Pfadausführung

Die Pfadausführung soll den geplanten Pfad übernehmen und das efeuLog- Fahrzeug vom Start zum Ziel bringen. Ein Pfad besteht aus einer Reihe von Wegpunkten, welche nacheinander abgefahren werden sollen, um das Fahrzeug vom Start zum Ziel zu bewegen.

Außerdem können auf Wegpunkten und Verbindungskanten bestimmte Fahrverhalten vorgegeben sein. Die Fahrverhalten beziehen sich in der Regel auf das Umfahren dynamischer Hindernisse oder dienen der Koordination der Multi-Roboter Navigation.

Als Trajektorie wird eine Kurve bezeichnet, die sämtliche Kurven einer gegebenen Kurvenschar unter gleichbleibenden Winkel schneidet.

Um eine sichere und reibungslose Fahrt zu realisieren, soll eine Trajektorie mit Berücksichtigung der kinematischen Einschränkungen berechnet werden. Außerdem sollen die Fahrtzeiten sowie die Abstände zu Hindernissen bei der Trajektorien- Planung berücksichtigt und optimiert werden.

Während die Trajektorien-Planung lediglich die maximale Geschwindigkeit begrenzt und sicherstellt, dass bspw. Fliehkräfte begrenzt werden, um eine sichere Fahrt zu garantieren, so begrenzt die Trajektorien- Ausführung diese geplanten Geschwindigkeiten weiter, um aktuelle Verkehrsregeln zu berücksichtigen oder dynamische Hindernisse sicher zu passieren.

Nachdem eine Trajektorie geplant wurde, soll das Fahrzeug diese Trajektorie so präzise wie möglich verfolgen. Dafür soll eine Regelungskomponente eingesetzt werden, um das Fahrzeug zu steuern. Diese soll zu jedem Zeitpunkt einen Geschwindigkeitsvektor berechnen, welcher durch mögliche Hindernisse oder Kurven begrenzt wird. 

Wie läuft die Pfadausführung ab?

Im nächsten Schritt muss aus diesen Wegpunkten und dem daraus resultierenden Pfad eine vom Fahrzeug ausführbare Trajektorie berechnet werden. Diese ist abhängig von den speziellen Fahrzeugeigenschaften sowie auch von eventuellen Beschränkungen des Fahrverhaltens auf den Pfadabschnitten (begrenzte Geschwindigkeit, etc.).Zuletzt wird mit Hilfe der Trajektorienausführung kontinuierlich ein Geschwindigkeitsvektor erzeugt, der an die Motorsteuerung weitergegeben wird und wodurch das Fahrzeug der bestimmten Trajektorie folgt. Dieser Geschwindigkeitsvektor ist abhängig sowohl von dem gewünschten Fahrweg als auch dem durch die Motorsteuerung zurückgegebenen Feedback über die real erzeugte Bewegung des Fahrzeugs.

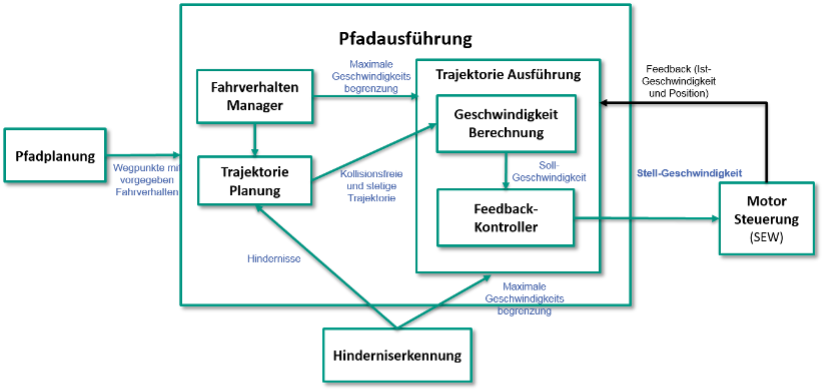
Die Kernaufgabe der Pfadausführung ist es, eine kollisionsfreie und glatte Trajektorie zu planen und präzise zu verfolgen. Hierfür gibt es verschiedener Verfahren.

Trajektorienmanagement-System

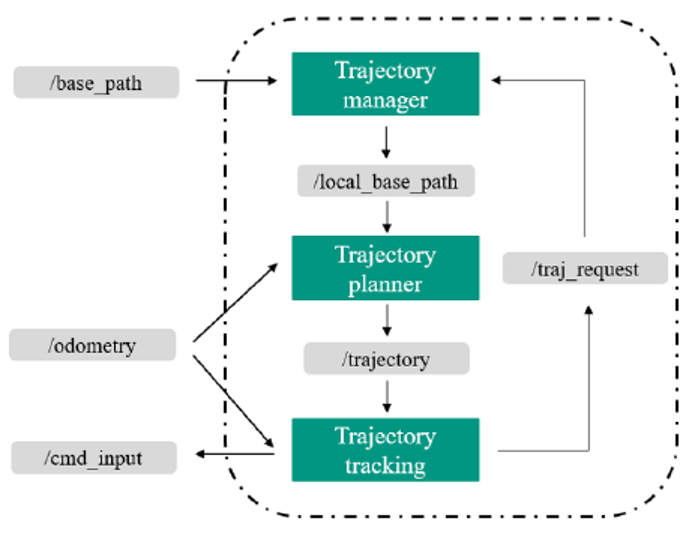
Die Abbildung zeigt den Aufbau des verwendeten Trajektorienmanagement-Systems. Der als „base_path“ bezeichnete Eingang beinhaltet den durch die Pfadplanung bestimmten Pfad bestehend aus einer Abfolge von Wegpunkten. 

Der Trajektorienmanager überprüft zunächst, ob der übergebene Pfad eine kollisionsfreie Trajektorie um detektierte Hindernisse zulässt. 

Um die Rechenzeit zu verringern, wird in der Trajektorienplanung jeweils nur eine Teilmenge bestehend aus den nächsten Wegpunkten („local_base_path“) betrachtet und für diese eine ausführbare Trajektorie berechnet. 

Die Trajektorie beinhaltet zwei Komponenten, zum einen den berechneten Fahrweg mit kontinuierlicher Krümmung sowie ein Geschwindigkeitsprofil entlang dieses Fahrwegs, der alle Restriktionen bezüglich Geschwindigkeit und Beschleunigungen erfüllt.

Aus dieser Trajektorie sowie dem durch die Odometrie rückgemeldete Pose (bzw. zurückgelegtem Weg) des Fahrzeugs („odometry“) werden kontinuierlich Fahrbefehle erzeugt, die dann an die Motorsteuerung („cmd_input“) weitergegeben werden.

Trajektoren- Planungsverfahren

Nachdem die Pfadplanung den optimalen Pfad ermittelt hat, muss eine Trajektorie berechnet werden, welche die kinematischen- sowie sicherheitsrelevanten Bedingungen berücksichtigt. Damit eine sichere und reibungslose Fahrt gewährleistet wird, verwendet man geometrische Funktionstypen, die als Trajektorien-Modell dienen, um die einzelnen Pfadpunkte zu verbinden. Die Parameter des Trajektorien-Modells werden anschließend optimiert, um die Fahrtzeiten, Fliehkräfte oder auch mögliche Abstände zu Objekten zu minimieren.

Für die Berechnung von Trajektorien wurden im Laufe der Zeit unterschiedliche Funktionstypen untersucht. Dazu zählen:
Klothoide (Broggi, Medici, Zani, Coati, & Panciroli, 2012) sind stetige Kurven die sich spiralförmig um zwei Konvergenzpunkte winden. Die auch als Cornu-Spirale bekannte Funktion besitzt die Eigenschaft, dass die Krümmung an jeder Stelle der Kurve proportional zur Länge ihres Bogens bis zu der Stelle ist. Schon früh wurde Klothoide für die Planung von Straßen verwendet. Durch ihren linear wachsenden Krümmungsverlauf ergibt sich ein konstanter Ruck beim Übergang von der Geradeausfahrt in die Kreisfahrt.

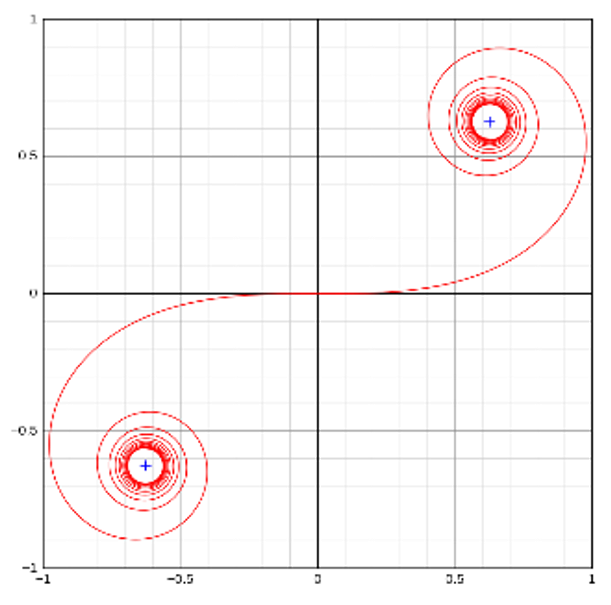
Polynomielle Spiralen (McNaughton, Urmson, Dolan, & Lee, 2011) (Gu, Snider, Dolan, & Lee, 2013) sind eine Verallgemeinerung der Cornu-Spirale. Durch die Verallgemeinerung ist der lineare Zusammenhang zwischen der Krümmung der Kurve und der Bogenlänge nichtmehr zwingend gegeben. Daraus folgend lassen sich durch Polynomielle Spiralen, verglichen mit Klothoiden eine größere Menge an möglichen Trajektorien erzeugen.

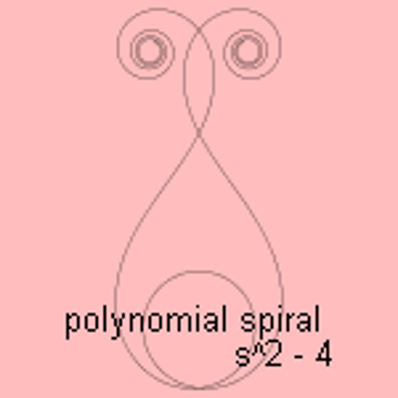
Bézierkurven (Bae, Moon, Park, Kim, & Kim, 2013) sind parametrisch modellierte, polynomielle Kurven. Eine Bézierkurve B(t) besitzt Grad n, wenn der Funktion n+1 Kontrollpunkte zugrunde liegen. Anfang und Ende der Kurve werden durch den ersten und letzten Kontrollpunkt festgelegt. Die Menge aller Kontrollpunkte bilden ein Polygon, welches die Gestalt der Kurve beeinflusst. Bézierkurven sind effizient zu berechnen und werden wegen ihrer eleganten Handhabung in vielen Disziplinen genutzt.

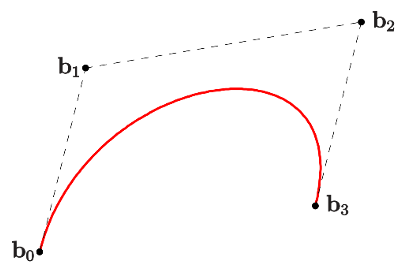
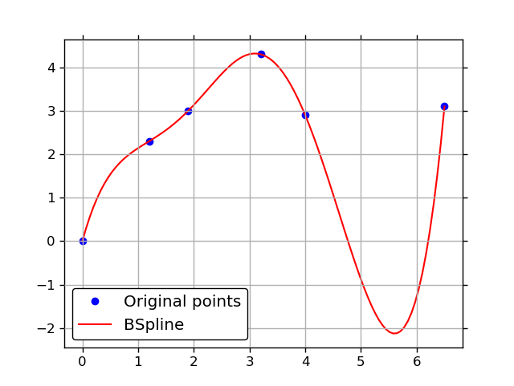
Eine Generalisierung von Bézierkurven sind Splines (Hardy & Campbell, 2013) (Kala & Warwick, 2013). Hierbei wird die gesamte Funktion abschnittsweise durch einzelne Polynome gebildet. An den angrenzenden Stellen der Funktionen (Knoten) können unterschiedliche Bedingungen gelten, um stetige Differenzierbarkeit zu gewährleisten. Splines beinhalten im Allgemeinen eine komplexere Theorie wie Bézierkurven und benötigen mehr Informationen, um sie zu bestimmen. Obwohl die Definition von Splines eine flexiblere Handhabung bietet, ist zu beachten, dass jeder Spline durch Bézierkurven dargestellt werden kann. Darüber hinaus sind Splines Polynome, was mit sich bringt, dass bspw. das Bilden von perfekten Kreisen unmöglich ist.

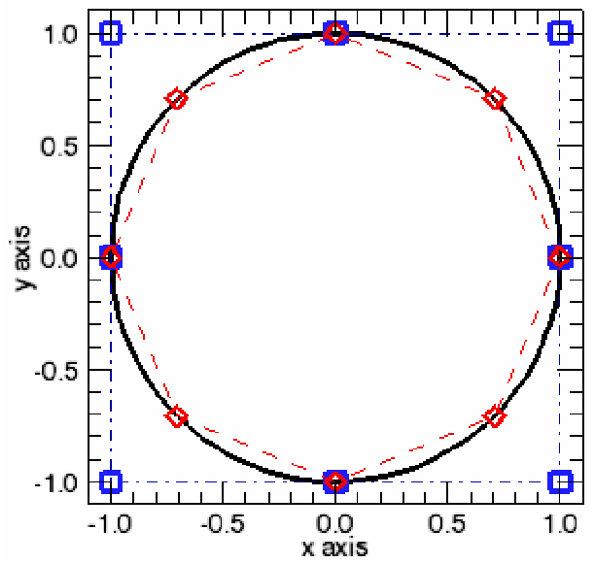
Bézierkurven und Splines bspw. unmöglich ist, einen perfekten Kreis abzubilden, kann ein NURBS jeden beliebigen stetigen Linienzug darstellen.

Distanz- Optimales Navigieren

Damit die geplante Trajektorie möglichst glatt und sicher ist, sollten die Abstände zu statischen Objekten maximiert werden. Durch die Einhaltung von Mindestabständen sowie das weiträumige Umfahren von Objekten verbessern sich die Sichtbedingungen. Darüber hinaus gleichzeitig auch die Anzahl von Bremsmanövern minimiert und Kurvenfahrten geglättet.
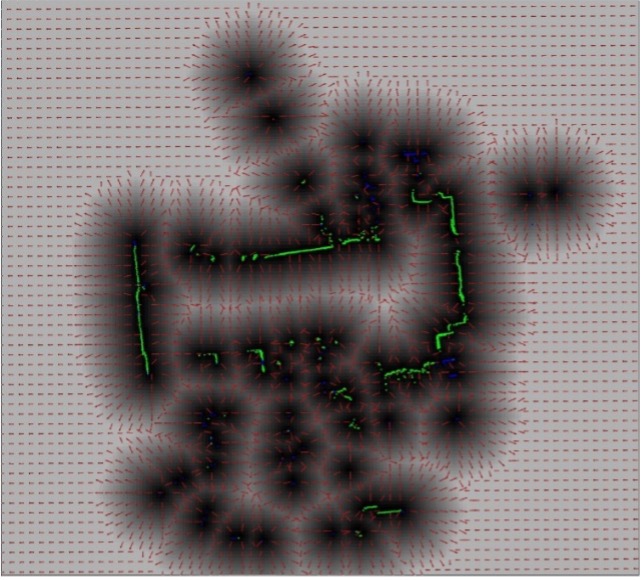
Eine Möglichkeit dieses Problem zu lösen, ist die Berücksichtigung des Voronoi-Diagrams (Choset & Burdick, 2000) der Umgebung. Der Voronoi-Diagram einer Umgebungskarte zerlegt den Raum in Zellen, sodass die Kanten des entstehenden Graphs die Abstände zu umliegenden Objekten maximieren und Objekte im Zentrum jeder Zelle liegen. Da die Berechnung jedoch rechenintensiv ist, wird auf vereinfachende Methoden zurückgegriffen. 

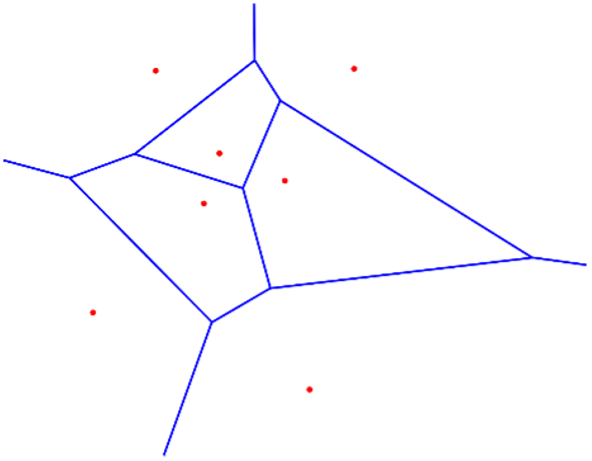
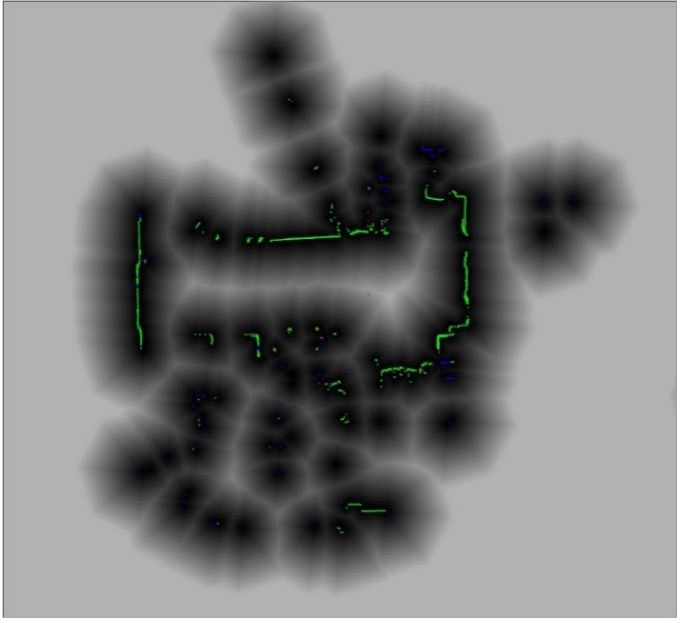
Als Grundlage für derartige Optimierungen wird eine Distanz-Karte berechnet. Diese Distanz-Karte beschreibt für jeden Punkt (x, y) im Raum den direkten Abstand zum nächstgelegenen Hindernis. 

Betrachtet man die lokalen Maxima der Distanz-Karte (Lau, Sprunk, & Burgard, 2010), dann ergibt sich eine Voronoi-ähnliche Struktur (Abbildung 8). Für ein optimales Fahrverhalten, wird die Trajektorie möglichst nah an diese Kanten geführt.

Konzept der Pfadausführung

Trajektoren- Planung mit quintischer Bézier- Spline

Das efeuLog- Fahrzeug ist mit einem Differentialantrieb ausgestattet. Um eine glatte Fahrt zu gewährleisten, muss die Krümmung der geplanten Trajektorie stetig sein. Das bedeutet, dass die erste und zweite Ableitung der gesamten Trajektorie stetig sein muss. Das fordert eine C²-Kontinuität (Bartels, Beatty, & Barsky, 1987) für die gesamte Trajektorie. 

Darüber hinaus müssen die Abstände der Trajektorie zu Hindernissen während der Planung überprüft werden. Daraus entsteht eine Anforderung an die Rechenlaufzeit: die Rechenlaufzeit bei der Trajektorie-Planung darf nicht länger als 1 Sekunde sein. Aufgrund der beiden Anforderungen, wird ein quintischer Bézier-Spline für die Trajektorien Planung eingesetzt.

Ein quintischer Bézier-Spline ist eine Funktion, die stückweise aus quintischen Bézierkurven (mit Grad 5) zusammengesetzt ist. Bei quintischen Bézierkurven, gilt die C²-Kontinuität nicht nur für die einzelnen Kurven, sondern auch an den Stellen, an denen zwei Bézierkurven zusammenstoßen. Dadurch erfüllt der gesamte Spline die C²-Kontinuität Anforderung. Außerdem können quintische Bézierkurven aufgrund ihrer mathematischen Eleganz, effizient berechnet werden. Somit stellen Splines ein wichtiges Werkzeug bei der Einhaltung von Berechnungsdauern dar.

Trajektoren- Ausführung mit Feedback- Kontroller

Die berechnete Trajektorie wird an eine Ausführungskomponente weitergeleitet. Die Ausführungskomponente berechnet zuerst die optimale Soll-Geschwindigkeit des Transportfahrzeugs mit den in vordefinierten Bedingungen. Bei der Berechnung werden die aktuelle Fahrgeschwindigkeit, die maximale Beschleunigung des Fahrzeugs, und die von der Hinderniserkennung und von Verkehrsregeln angegebenen maximale Geschwindigkeit berücksichtigt, um einen zeitoptimale Soll-Geschwindigkeitsvektoren zu jedem Zeitpunkt zu planen.

Für die Fahrzeugregelung wird ein Feedback-Kontroller eingesetzt, um die geplante Soll-Geschwindigkeit möglich präzise einzuhalten. Dabei wird die Regelabweichung zwischen Soll-Geschwindigkeit und Ist-Geschwindigkeit des Fahrzeugs abgeglichen und eine Stell-Geschwindigkeit berechnet. Diese Stell-Geschwindigkeit wird dann an die SEW Motorsteuerung weitergeleitet.

Schnittstelle zur Motor- Steuerung

Der Feedback-Kontroller schickt den Stell-Geschwindigkeitsvektor an die SEW Motorsteuerung und bekommt Feedback, bestehend aus der Ist-Geschwindigkeit und der Position, zurück. Hierfür muss eine Schnittstelle zwischen dem Feedback-Kontroller und der Motorsteuerung definiert werden, die dann zusammen mit der SEW- Eurodrive implementiert wird.

Trajektoren- Neuplanung

Wegen mechanischer und technischer Einschränkungen kann die Soll-Geschwindigkeit nicht immer exakt geregelt werden. Das führt zu einer Positionsabweichung während der Trajektorien- Ausführung. Falls diese Abweichung zu groß ist, kann der geplante Pfad nicht mehr präzise verfolgt werden, was zu einer lokalen Kollision oder Verkehrsverstößen führen könnte.

Deshalb muss die gesamte Trajektorie komplett neu geplant werden, falls die Abweichung zur geplanten Trajektorie eine vordefinierte Fehlerschranke überschritten hat. Solche Fehlerschranken werden in der Praxis experimentell bestimmt und festgelegt.

Es kann passieren, dass bei einer Neuplanung keine kollisionsfreie und stetige Trajektorie gefunden werden kann. In diesem Fall soll die Fehlermeldung zuerst an das Leitsystem weitergeleitet werden, um auf Anweisungen zur Fehlerbehandlung zu warten.